个人随笔
目录
Java实现图连通网的最小生成树算法之Prim算法
2020-05-08 23:21:50

摘要：图，连通网，最小生成树，Prim算法，Java实现Prim

一、相关概念

首先，我们得理解啥是最小生成树以及图的相关定义

  • 连通图：在无向图中，若任意两个顶点vi与vj都有路径相通，则称该无向图为连通图。
  • 强连通图：在有向图中，若任意两个顶点vi与vj都有路径相通，则称该有向图为强连通图。
  • 连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
  • 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
  • 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

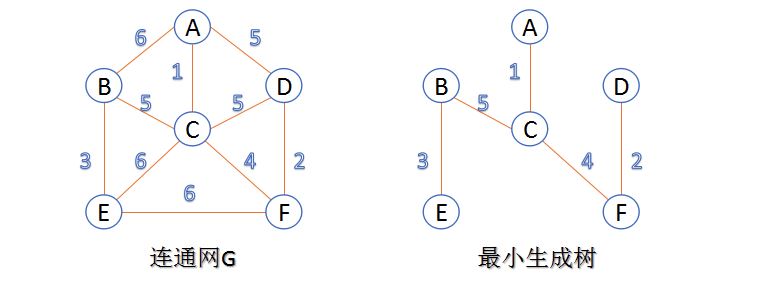
由上可知，最小生成树是对于连通网的，举个例子，如下所示：

我们知道，最小生成树的算法通常有两种：Kruskal算法和Prim算法。这两种算法都是属于贪心算法。这篇博文研究的是Prim算法。

二、最小生成树的形成

怎么找到最小生成树呢，其实不管是Kruskal算法还是Prim算法都是一个原理：找到一条轻量级边，举个简单例子，我们一个联通图的节点集合Q，和他的最小生成树A，那么树A中的节点与集合Q中的权重最小的边就为轻量级边，该轻量级边横跨了集合Q和树A，一定是属于最小生成树的，所以可以把该轻量级边在Q中的节点加入到最小生成树A中。具体原理以及证明请查看：算法导论第三版第六部分图算法最小生成树（625~628页）。因为篇幅原因，这里不做过多说明，总之Kruskal和Prim都是基于这个原理的。

三、Prim算法

Prim算法可以称为是“加点法”，不过本质上还是选择一条轻量级边，它具有的一个性质是集合A中的边总是构成一颗树。这棵树从一个任意的根节点r开始，一直长大到覆盖V中的所有节点位置。算法每一步在连接集合A和A之外的节点的所有边中，选择一条轻量级边加入到A中。本策略属于贪心策略，因为每一步所加入的边都必须是使树的总权重增加量最小的边。

算法伪代码如下：

  1. MST-PRIM(G,w,r)
  2.     for each u <- G.V
  3.         u.key=∞
  4.         u.π =NIL
  5.     r:key=0
  6.     Q=G.V
  7.     while Q≠O
  8.         u=EXTRACT-MIN(Q)
  9.         for each v <- G.Adj[u]
  10.         if v<-Q and w(u,v)<v.key
  11.            v.π=u
  12.            v.key=w(u,v)
  13.            DECREASE-KEY(Q,v)
  14.         A=A∪{u}

在上面的伪代码中，所有不在树A中的节点全部都存放在一个基于key属性的最小优先队列Q中，对于每个节点v，属性v.key保存的是连接v和树中节点所有边中最小权重的边，我们约定若不存在这样子的边，则u.key=∞。属性v.π给出的是节点v在树中的父节点。

举个例子

有如下连通网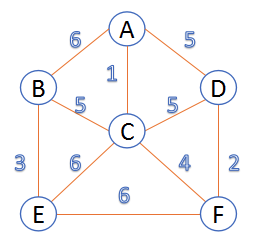

根据上面的伪代码来运行

第一步：初始化A和优先队列Q
  1. A={},Q={A,B,C,D,E,F}
  2. A.Key=0;A.π=Nil
  3. B.Key=∞;B.π=Nil
  4. C.Key=∞;C.π=Nil
  5. D.Key=∞;D.π=Nil
  6. E.Key=∞;E.π=Nil
  7. F.Key=∞;F.π=Nil
第二步：从Q中取出A来，更新各个节点到树A的距离，以及保证Q还是优先队列
  1. A={A},Q={C,B,D,E,F}
  2. A.key=0;A.π=NIL
  4. B.key=6;B.π=A
  5. C.key=1;C.π=A
  6. D.key=5;D.π=A
  7. E.key=∞;E.π=NIL
  8. F.key=∞;F.π=NIL
第三步：从Q中取出C来，更新各个节点到树A的距离，以及保证Q还是优先队列
  1. A={A,C},Q={F,B,D,E}
  2. A.key=0;A.π=NIL
  3. C.key=1;C.π=A
  5. B.key=5;B.π=C
  6. D.key=5;D.π=A
  7. E.key=6;E.π=C
  8. F.key=4;F.π=C
第四步：从Q中取出F来，更新各个节点到树A的距离，以及保证Q还是优先队列
  1. A={A,C,F},Q={D,B,E}
  2. A.key=0;A.π=NIL
  3. C.key=1;C.π=A
  4. F.key=4;F.π=C
  6. B.key=5;B.π=C
  7. D.key=2;D.π=F
  8. E.key=6;E.π=C
第五步：从Q中取出D来，更新各个节点到树A的距离，以及保证Q还是优先队列
  1. A={A,C,F,D},Q={B,E}
  2. A.key=0;A.π=NIL
  3. C.key=1;C.π=A
  4. F.key=4;F.π=C
  5. D.key=2;D.π=F
  7. B.key=5;B.π=C
  8. E.key=6;E.π=C
第七步：从Q中取出B来，更新各个节点到树A的距离，以及保证Q还是优先队列
  1. A={A,C,F,D，B},Q={E}
  2. A.key=0;A.π=NIL
  3. C.key=1;C.π=A
  4. F.key=4;F.π=C
  5. D.key=2;D.π=F
  6. B.key=5;B.π=C
  8. E.key=3;E.π=B
第八步：从Q中取出E来，更新各个节点到树A的距离，以及保证Q还是优先队列
  1. A={A,C,F,D,B,E},Q={}
  2. A.key=0;A.π=NIL
  3. C.key=1;C.π=A
  4. F.key=4;F.π=C
  5. D.key=2;D.π=F
  6. B.key=5;B.π=C
  7. E.key=3;E.π=B
第九步：Q为空，结束。

由上面可以知道，根据伪代码中的逻辑，成功生产了图的最小生成树，我们现在聊分析下算法的复杂度！

四、Prim算法时间复杂度分析

我们现在来重新砍一下Prim算法，把上面的伪代码拷贝下来

  1. MST-PRIM(G,w,r)
  2.     for each u <- G.V
  3.         u.key=∞
  4.         u.π =NIL
  5.     r:key=0
  6.     Q=G.V
  7.     while Q≠O
  8.         u=EXTRACT-MIN(Q)
  9.         for each v <- G.Adj[u]
  10.         if v<-Q and w(u,v)<v.key
  11.            v.π=u
  12.            v.key=w(u,v)
  13.            DECREASE-KEY(Q,v)
  14.         A=A∪{u}

算法的2~6行是建堆，我们知道最小优先队列的初始化时间成本为O(V）。因为有V个节点，所以while循环要执行V次，从最小优先队列中取出堆顶元素时间成本为O(lgV),所以第8行的总时间成本为O(VlgV)。因为邻接矩阵的边为2E，所以9~13行总执行次数为O(E)，在for循环里，我们可以在常数时间里完成对一个节点是否属于Q，方法就是对每个节点维护一个标志位来指明该节点是否属于Q，并在将节点从Q中删除的时候对该标志位进行更新。在算法12行因为改变了节点的key值，所以需要重新建堆，该操作在二叉最小堆上执行的时间成本为O(lgV)。因此第9~13行的总执行时间成本为O(ElgV)。所以Prim算法的总时间代价为O(V+VlgV+ElgV)=O(ElgV)。如果用斐波那契堆来实现最小优先队列Q，Prim算法的渐进运行时间可以进一步得到改善。

五、Java实现

我们这里用Java来实现Prim算法，根据上面的伪代码我们知道，我们需要实现一个最小优先队列，这里用最小堆来实现，代码如下：

  1. /**
  2.  *最小堆实现的一个优先队列
  3. * @author suibibk@qq.com
  4. */
  5. class PriorityQueue<E extends Comparable<E>> {
  6.     //这里使用数组来实现
  7.     private ArrayList<E> data;
  9.     public PriorityQueue(int capacity) {
  10.         data = new ArrayList<>(capacity);
  11.     }
  12.     public PriorityQueue() {
  13.         data  = new ArrayList<>();
  14.     }
  16.     //返回堆中元素的个数
  17.     public int getSize() {
  18.         return data.size();
  19.     }
  21.     //返回二叉树中索引为index的节点的父节点索引
  22.     public int parent(int index) {
  23.         if(index == 0) {
  24.             throw new IllegalArgumentException("index-0 dosen't have parent");
  25.         }
  26.         return (index-1)/2;
  27.     }
  29.     //返回完全二叉树中索引为index的节点的左孩子的索引
  30.     private int leftChild(int index) {
  31.         return index*2+1;
  32.     }
  34.     //返回完全二叉树中索引为index的节点的右孩子的索引
  35.    private int rightChild(int index) {
  36.        return index * 2 + 2;
  37.    }
  38.    //交换索引为i、j的值
  39.    private void swap(int i, int j) {
  40.        E t = data.get(i);
  41.        data.set(i, data.get(j));
  42.        data.set(j, t);
  43.    }
  45.    //向堆中添加元素
  46.    public void add(E e) {
  47.        data.add(e);
  48.        siftUp(data.size() - 1);
  49.    }
  50.    //上浮
  51.    private void siftUp(int k) {
  52.        //k不能是根节点，并且k的值要比父节点的值小
  53.        while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) > 0) {
  54.            swap(k, parent(k));
  56.            k = parent(k);
  57.        }
  58.    }
  60.  //看堆中最小的元素
  61.    public E findMin() {
  62.        if (data.size() == 0)
  63.            throw new IllegalArgumentException("Can not findMax when heap is empty");
  64.        return data.get(0);
  65.    }
  67.    //取出堆中最小的元素
  68.    public E extractMin() {
  69.        E ret = findMin();
  71.        swap(0, data.size() - 1);
  72.        data.remove(data.size() - 1);
  73.        siftDown(0);
  75.        return ret;
  76.    }
  77.    /**
  78.     * 当修改了堆中一些元素后,要执行先向下浮再向上浮的操作，这里需要重新建堆
  79.     */
  80.    public void rebuildHead(E e) {
  81.       // 这里优化为在建优先队列的时候，就指定节点在优先队列中的坐标，那么就不需要使用循环
  82.        for (int j = 0; j < data.size(); j++) {
  83.             if(e==data.get(j)) {
  84.                 siftDown(j);
  85.                  siftUp(j);
  86.                 break;
  87.             }
  88.        }
  90.    }
  91.    //下浮
  92.    private void siftDown(int k) {
  93.        //leftChild存在
  94.        while (leftChild(k) < data.size()) {
  95.            int j = leftChild(k);
  96.            //rightChild存在,且值小于leftChild的值
  97.            if (j + 1 < data.size() &&
  98.                    data.get(j).compareTo(data.get(j + 1)) > 0)
  99.                j = rightChild(k);
  100.            //data[j]是leftChild和rightChild中最小的
  101.            if (data.get(k).compareTo(data.get(j)) <0)
  102.                break;
  104.            swap(k, j);
  105.            k = j;
  106.        }
  108.    }
  110.    //取出堆中最大的元素,替换为元素e
  111.    public E replace(E e){
  112.        E ret = findMin();
  114.        data.set(0, e);
  115.        siftDown(0);
  117.        return ret;
  118.    }
  120.  //heapify操作:将数组转化为堆
  121.   public PriorityQueue(E[] arrs) {
  122.        data = new ArrayList<>(Arrays.asList(arrs));
  123.        for (int i = parent(data.size() - 1); i >= 0; i--) {
  124.            siftDown(i);
  125.        }
  126.    }
  128.    public void print() {
  129.        for (E e : data) {
  130.             System.out.print(" "+e);
  131.         }
  132.    }
  134.    public List<E> getDate() {
  135.        return data;
  136.    }
  137. }

该队列初始化的复杂度为O(V)，取出队头的复杂度为O(lgV),重新建堆的复杂度为O(lgV)，满足伪代码中的要求。

然后我们需要有一个节点对象，该对象不仅仅是当做图的节点，还要当做树A中的节点以及最小优先队列Q中的节点，所以不仅仅需要节点名称，还需要父节点，以及key属性，以及一个标志位表明是否存在Q中（这是为了让这个判定复杂度变为O(1)）。

  1. //图的节点，当然也是最小优先队列Q的节点，也是最小生成树A的节点：因此多了属性key，parent，inQ
  2. class Node implements Comparable<Node>{
  3.     private int index;//坐标
  4.     private int  key;//每个节点的key属性
  5.     private String value;//节点名称
  6.     private Node parent;//父节点
  7.     private int inQ=1;//是否属于Q，默认是属于的，等离开才不属于
  8.     @Override
  9.     public int compareTo(Node o) {
  10.         return this.key-o.key;
  11.     }
  12.     public Node(String value) {
  13.         super();
  14.         this.value = value;
  15.     }
  17.     public int getIndex() {
  18.         return index;
  19.     }
  20.     public void setIndex(int index) {
  21.         this.index = index;
  22.     }
  23.     public int getKey() {
  24.         return key;
  25.     }
  26.     public void setKey(int key) {
  27.         this.key = key;
  28.     }
  29.     public String getValue() {
  30.         return value;
  31.     }
  32.     public void setValue(String value) {
  33.         this.value = value;
  34.     }
  35.     public Node getParent() {
  36.         return parent;
  37.     }
  38.     public void setParent(Node parent) {
  39.         this.parent = parent;
  40.     }
  41.     public int getInQ() {
  42.         return inQ;
  43.     }
  44.     public void setInQ(int inQ) {
  45.         this.inQ = inQ;
  46.     }
  47. }

然后我们需要一个图对象，可以方便的通过某一个节点找到相邻的节点，这里用的是邻接矩阵来存储图：

  1. //定义图：无向图
  2. class Graph{
  3.     //顶点数目
  4.     int size;
  5.     int index=0;
  6.     //顶点
  7.     private List<Node> vertexs;
  8.     //边
  9.     int[][] edges;
  10.     //初始化
  11.     public Graph(int size) {
  12.         this.size=size;
  13.         this.vertexs=new ArrayList<Node>(size);
  14.         this.edges=new int[size][size];
  16.     }
  17.     //添加顶点
  18.     public void addVertex(Node node) {
  19.         node.setIndex(index);
  20.         vertexs.add(node);
  21.         index++;
  22.     }
  23.     //添加边:有权重有方向
  24.     public void addEdge(Node vertex1,Node vertex2,int weight) {
  25.         //因为是无向图，所以这里直接把两条边都加上
  26.         edges[vertex1.getIndex()][vertex2.getIndex()]=weight;
  27.         edges[vertex2.getIndex()][vertex1.getIndex()]=weight;
  28.     }
  30.     public List<Node> getVertexs() {
  31.         return vertexs;
  32.     }
  33.     /***************上面已经做好了图，现在做遍历********************/
  34.     /**
  35.      * 打印图
  36.      * @param index
  37.      */
  38.     public void printGraph() {
  39.         System.out.print("图\t ");
  40.         for (Node vertex: vertexs) {
  41.             System.out.print(vertex.getValue()+"\t");
  42.         }
  43.         System.out.println("\n");
  44.         for (int i = 0; i <size; i++) {
  45.             Node vertex = vertexs.get(i);
  46.             System.out.print(vertex.getValue()+"\t");
  47.             for (int j = 0; j < size; j++) {
  48.                 System.out.print(edges[i][j]+"\t");
  49.             }
  50.             System.out.println("\n");
  51.         }
  52.         System.out.println();
  53.     }
  54.     /**
  55.      * 获取节点index相邻的节点
  56.      * @param index
  57.      * @return
  58.      */
  59.     public List<Node> getAdjacentVertexIndex(Node node) {
  60.         List<Node> lists = new ArrayList<Node>();
  61.         for (int j = 0; j < size; j++) {
  62.             if(edges[node.getIndex()][j]!=0) {
  63.                 lists.add(vertexs.get(j));
  64.             }
  65.         }
  66.         return lists;
  67.     }
  68. }

上面都准备好了后，我们就可以根据伪代码中的逻辑来实现最小生成树啦！

  1. public static  List<Node> prim(Graph graph){
  2.         //1、初始化一个最小优先队列
  3.         PriorityQueue<Node> Q = new PriorityQueue<Node>();
  4.         //这里第一个顶点的key是0，其他都是Integer.MAX_VALUE 代表无穷
  5.         List<Node> nodes = graph.getVertexs();
  6.         for (int i = 0; i < nodes.size(); i++) {
  7.             Node node = nodes.get(i);
  8.             node.setParent(null);
  9.             if(i==0) {
  10.                 node.setKey(0);
  11.             }else {
  12.                 node.setKey(Integer.MAX_VALUE);
  13.             }
  14.             Q.add(node);
  15.         }
  16.         //2、初始化生成树A，一开始树A为空，全部节点都还在Q中
  17.         List<Node> A = new ArrayList<Node>();
  19.         /**
  20.          * 上面初始化最小堆的时间复杂度为O(V)
  21.          */
  22.         //3、开始执行逻辑
  23.         while(Q.getSize()!=0) {//这个要执行|V|次
  24.             //4、获取第一个节点
  25.             Node minNode = Q.extractMin();//这一步的时间复杂度是：O(VlgV)
  26.             //5、取出这个节点对应的连接边
  27.             List<Node> adjNodes = graph.getAdjacentVertexIndex(minNode);
  29.             for (int i = 0; i < adjNodes.size(); i++) {//这里要执行|E|次
  30.                 //6、检查该节点是否属于集合Q
  32.                 Node node = adjNodes.get(i);
  33.                 /**
  34.                  * 对每个节点维护一个标志位来指明该节点是否属于Q，
  35.                  * 并在将节点Q从Q中移除的时候将标志位进行更新,时间复杂度则为O(1)
  36.                  */
  38.                 if(node.getInQ()==1) {
  39.                     //7、获取这个邻接边的权重
  40.                     int weight = graph.edges[minNode.getIndex()][node.getIndex()];
  41.                     if(weight<node.getKey()) {
  42.                         //8、更新node的值
  43.                         node.setParent(minNode);
  44.                         //这一行操作涉及后面需要重新建堆
  45.                         node.setKey(weight);
  46.                         //重新建堆
  47.                         Q.rebuildHead(node);//这一步的时间复杂度是O(ElgV)
  48.                     }
  49.                 }
  50.             }
  51.             //10，将该节点加入集合A
  52.             minNode.setInQ(0);
  53.             A.add(minNode);
  54.         }
  55.         //所以时间复杂度为O(V+VlgV+ElgV)=O(ElgV)=O(ElgV)
  56.         return A;
  57.     }

好了，到这里就已经实现完了，把代码整合测试下：

Java实现Prim算法

  1. /**
  2.  * 连通无向图最小生成树Prim算法Java实现
  3.  * @author suibibk@qq.com
  4.  */
  5. public class Prim {
  6.     public static  List<Node> prim(Graph graph){
  7.         //1、初始化一个最小优先队列
  8.         PriorityQueue<Node> Q = new PriorityQueue<Node>();
  9.         //这里第一个顶点的key是0，其他都是Integer.MAX_VALUE 代表无穷
  10.         List<Node> nodes = graph.getVertexs();
  11.         for (int i = 0; i < nodes.size(); i++) {
  12.             Node node = nodes.get(i);
  13.             node.setParent(null);
  14.             if(i==0) {
  15.                 node.setKey(0);
  16.             }else {
  17.                 node.setKey(Integer.MAX_VALUE);
  18.             }
  19.             Q.add(node);
  20.         }
  21.         //2、初始化生成树A，一开始树A为空，全部节点都还在Q中
  22.         List<Node> A = new ArrayList<Node>();
  24.         /**
  25.          * 上面初始化最小堆的时间复杂度为O(V)
  26.          */
  27.         //3、开始执行逻辑
  28.         while(Q.getSize()!=0) {//这个要执行|V|次
  29.             //4、获取第一个节点
  30.             Node minNode = Q.extractMin();//这一步的时间复杂度是：O(VlgV)
  31.             //5、取出这个节点对应的连接边
  32.             List<Node> adjNodes = graph.getAdjacentVertexIndex(minNode);
  34.             for (int i = 0; i < adjNodes.size(); i++) {//这里要执行|E|次
  35.                 //6、检查该节点是否属于集合Q
  37.                 Node node = adjNodes.get(i);
  38.                 /**
  39.                  * 对每个节点维护一个标志位来指明该节点是否属于Q，
  40.                  * 并在将节点Q从Q中移除的时候将标志位进行更新,时间复杂度则为O(1)
  41.                  */
  43.                 if(node.getInQ()==1) {
  44.                     //7、获取这个邻接边的权重
  45.                     int weight = graph.edges[minNode.getIndex()][node.getIndex()];
  46.                     if(weight<node.getKey()) {
  47.                         //8、更新node的值
  48.                         node.setParent(minNode);
  49.                         //这一行操作涉及后面需要重新建堆
  50.                         node.setKey(weight);
  51.                         //重新建堆
  52.                         Q.rebuildHead(node);//这一步的时间复杂度是O(ElgV)
  53.                     }
  54.                 }
  55.             }
  56.             //10，将该节点加入集合A
  57.             minNode.setInQ(0);
  58.             A.add(minNode);
  59.         }
  60.         //所以时间复杂度为O(V+VlgV+ElgV)=O(ElgV)=O(ElgV)
  61.         return A;
  62.     }
  65.     /**
  66.      * 打印最小生成树的节点A
  67.      * @param graph 图 作用是找到节点名称
  68.      * @param A
  69.      */
  70.     public static void printPrim(List<Node> A) {
  71.         //这里就已经生成了最小生成树了，遍历输出A
  72.         for (int i = 0; i < A.size(); i++) {
  73.             Node node = A.get(i);
  74.             String vertex =  node.getValue();
  75.             Node parent = node.getParent();
  76.             String pVertex = "NIL";
  77.             if(parent!=null) {
  78.                 pVertex=parent.getValue();
  79.             }
  80.             System.out.println("节点："+vertex+";父节点："+pVertex+";权重："+node.getKey());
  81.         }
  82.     }
  84.     public static Graph getGraph() {
  85.         Graph graph = new Graph(6);
  86.         Node A = new Node("A");
  87.         Node B = new Node("B");
  88.         Node C = new Node("C");
  89.         Node D = new Node("D");
  90.         Node E = new Node("E");
  91.         Node F = new Node("F");
  93.         graph.addVertex(A);
  94.         graph.addVertex(B);
  95.         graph.addVertex(C);
  96.         graph.addVertex(D);
  97.         graph.addVertex(E);
  98.         graph.addVertex(F);
  100.         graph.addEdge(A, B,6);
  101.         graph.addEdge(A, D,5);
  102.         graph.addEdge(A, C,1);
  103.         graph.addEdge(B, C,5);
  104.         graph.addEdge(C, D,5);
  105.         graph.addEdge(B, E,3);
  106.         graph.addEdge(D, F,2);
  107.         graph.addEdge(C, F,4);
  108.         graph.addEdge(E, F,6);
  109.         graph.addEdge(E, C,6);
  110.         return graph;
  111.     }
  113.     public static void main(String[] args) {
  114.         //获取一个图
  115.         Graph graph = getGraph();
  116.         graph.printGraph();
  117.         //获取该图的最小生成树
  118.         List<Node> A = prim(graph);
  119.         printPrim(A);
  120.     }
  122. }
  123. //图的节点，当然也是最小优先队列Q的节点，也是最小生成树A的节点：因此多了属性key，parent，inQ
  124. class Node implements Comparable<Node>{
  125.     private int index;//坐标
  126.     private int  key;//每个节点的key属性
  127.     private String value;//节点名称
  128.     private Node parent;//父节点
  129.     private int inQ=1;//是否属于Q，默认是属于的，等离开才不属于
  130.     @Override
  131.     public int compareTo(Node o) {
  132.         return this.key-o.key;
  133.     }
  134.     public Node(String value) {
  135.         super();
  136.         this.value = value;
  137.     }
  139.     public int getIndex() {
  140.         return index;
  141.     }
  142.     public void setIndex(int index) {
  143.         this.index = index;
  144.     }
  145.     public int getKey() {
  146.         return key;
  147.     }
  148.     public void setKey(int key) {
  149.         this.key = key;
  150.     }
  151.     public String getValue() {
  152.         return value;
  153.     }
  154.     public void setValue(String value) {
  155.         this.value = value;
  156.     }
  157.     public Node getParent() {
  158.         return parent;
  159.     }
  160.     public void setParent(Node parent) {
  161.         this.parent = parent;
  162.     }
  163.     public int getInQ() {
  164.         return inQ;
  165.     }
  166.     public void setInQ(int inQ) {
  167.         this.inQ = inQ;
  168.     }
  169. }
  171. //定义图：无向图
  172. class Graph{
  173.     //顶点数目
  174.     int size;
  175.     int index=0;
  176.     //顶点
  177.     private List<Node> vertexs;
  178.     //边
  179.     int[][] edges;
  180.     //初始化
  181.     public Graph(int size) {
  182.         this.size=size;
  183.         this.vertexs=new ArrayList<Node>(size);
  184.         this.edges=new int[size][size];
  186.     }
  187.     //添加顶点
  188.     public void addVertex(Node node) {
  189.         node.setIndex(index);
  190.         vertexs.add(node);
  191.         index++;
  192.     }
  193.     //添加边:有权重有方向
  194.     public void addEdge(Node vertex1,Node vertex2,int weight) {
  195.         //因为是无向图，所以这里直接把两条边都加上
  196.         edges[vertex1.getIndex()][vertex2.getIndex()]=weight;
  197.         edges[vertex2.getIndex()][vertex1.getIndex()]=weight;
  198.     }
  200.     public List<Node> getVertexs() {
  201.         return vertexs;
  202.     }
  203.     /***************上面已经做好了图，现在做遍历********************/
  204.     /**
  205.      * 打印图
  206.      * @param index
  207.      */
  208.     public void printGraph() {
  209.         System.out.print("图\t ");
  210.         for (Node vertex: vertexs) {
  211.             System.out.print(vertex.getValue()+"\t");
  212.         }
  213.         System.out.println("\n");
  214.         for (int i = 0; i <size; i++) {
  215.             Node vertex = vertexs.get(i);
  216.             System.out.print(vertex.getValue()+"\t");
  217.             for (int j = 0; j < size; j++) {
  218.                 System.out.print(edges[i][j]+"\t");
  219.             }
  220.             System.out.println("\n");
  221.         }
  222.         System.out.println();
  223.     }
  224.     /**
  225.      * 获取节点index相邻的节点
  226.      * @param index
  227.      * @return
  228.      */
  229.     public List<Node> getAdjacentVertexIndex(Node node) {
  230.         List<Node> lists = new ArrayList<Node>();
  231.         for (int j = 0; j < size; j++) {
  232.             if(edges[node.getIndex()][j]!=0) {
  233.                 lists.add(vertexs.get(j));
  234.             }
  235.         }
  236.         return lists;
  237.     }
  238. }
  239. /**
  240.  *最小堆实现的一个优先队列
  241. * @author suibibk@qq.com
  242. */
  243. class PriorityQueue<E extends Comparable<E>> {
  244.     //这里使用数组来实现
  245.     private ArrayList<E> data;
  247.     public PriorityQueue(int capacity) {
  248.         data = new ArrayList<>(capacity);
  249.     }
  250.     public PriorityQueue() {
  251.         data  = new ArrayList<>();
  252.     }
  254.     //返回堆中元素的个数
  255.     public int getSize() {
  256.         return data.size();
  257.     }
  259.     //返回二叉树中索引为index的节点的父节点索引
  260.     public int parent(int index) {
  261.         if(index == 0) {
  262.             throw new IllegalArgumentException("index-0 dosen't have parent");
  263.         }
  264.         return (index-1)/2;
  265.     }
  267.     //返回完全二叉树中索引为index的节点的左孩子的索引
  268.     private int leftChild(int index) {
  269.         return index*2+1;
  270.     }
  272.     //返回完全二叉树中索引为index的节点的右孩子的索引
  273.    private int rightChild(int index) {
  274.        return index * 2 + 2;
  275.    }
  276.    //交换索引为i、j的值
  277.    private void swap(int i, int j) {
  278.        E t = data.get(i);
  279.        data.set(i, data.get(j));
  280.        data.set(j, t);
  281.    }
  283.    //向堆中添加元素
  284.    public void add(E e) {
  285.        data.add(e);
  286.        siftUp(data.size() - 1);
  287.    }
  288.    //上浮
  289.    private void siftUp(int k) {
  290.        //k不能是根节点，并且k的值要比父节点的值小
  291.        while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) > 0) {
  292.            swap(k, parent(k));
  294.            k = parent(k);
  295.        }
  296.    }
  298.  //看堆中最小的元素
  299.    public E findMin() {
  300.        if (data.size() == 0)
  301.            throw new IllegalArgumentException("Can not findMax when heap is empty");
  302.        return data.get(0);
  303.    }
  305.    //取出堆中最小的元素
  306.    public E extractMin() {
  307.        E ret = findMin();
  309.        swap(0, data.size() - 1);
  310.        data.remove(data.size() - 1);
  311.        siftDown(0);
  313.        return ret;
  314.    }
  315.    /**
  316.     * 当修改了堆中一些元素后,要执行先向下浮再向上浮的操作，这里需要重新建堆
  317.     */
  318.    public void rebuildHead(E e) {
  319.       // 这里优化为在建优先队列的时候，就指定节点在优先队列中的坐标，那么就不需要使用循环
  320.        for (int j = 0; j < data.size(); j++) {
  321.             if(e==data.get(j)) {
  322.                 siftDown(j);
  323.                  siftUp(j);
  324.                 break;
  325.             }
  326.        }
  328.    }
  329.    //下浮
  330.    private void siftDown(int k) {
  331.        //leftChild存在
  332.        while (leftChild(k) < data.size()) {
  333.            int j = leftChild(k);
  334.            //rightChild存在,且值小于leftChild的值
  335.            if (j + 1 < data.size() &&
  336.                    data.get(j).compareTo(data.get(j + 1)) > 0)
  337.                j = rightChild(k);
  338.            //data[j]是leftChild和rightChild中最小的
  339.            if (data.get(k).compareTo(data.get(j)) <0)
  340.                break;
  342.            swap(k, j);
  343.            k = j;
  344.        }
  346.    }
  348.    //取出堆中最大的元素,替换为元素e
  349.    public E replace(E e){
  350.        E ret = findMin();
  352.        data.set(0, e);
  353.        siftDown(0);
  355.        return ret;
  356.    }
  358.  //heapify操作:将数组转化为堆
  359.   public PriorityQueue(E[] arrs) {
  360.        data = new ArrayList<>(Arrays.asList(arrs));
  361.        for (int i = parent(data.size() - 1); i >= 0; i--) {
  362.            siftDown(i);
  363.        }
  364.    }
  366.    public void print() {
  367.        for (E e : data) {
  368.             System.out.print(" "+e);
  369.         }
  370.    }
  372.    public List<E> getDate() {
  373.        return data;
  374.    }
  375. }

输入上面的图，运行结果如下：

  1. 图     A    B    C    D    E    F    
  3. A    0    6    1    5    0    0    
  5. B    6    0    5    0    3    0    
  7. C    1    5    0    5    6    4    
  9. D    5    0    5    0    0    2    
  11. E    0    3    6    0    0    6    
  13. F    0    0    4    2    6    0    
  16. 节点：A;父节点：NIL;权重：0
  17. 节点：C;父节点：A;权重：1
  18. 节点：F;父节点：C;权重：4
  19. 节点：D;父节点：F;权重：2
  20. 节点：B;父节点：C;权重：5
  21. 节点：E;父节点：B;权重：3

可以看到结果跟伪代码执行逻辑结果是一样的，大功搞成！要了老命，这篇笔记写了6个钟！

 2262

啊！这个可能是世界上最丑的留言输入框功能~


当然，也是最丑的留言列表

有疑问发邮件到 : suibibk@qq.com 侵权立删
Copyright : 个人随笔   备案号 : 粤ICP备18099399号-2