图的深度优先搜索(DFS)和广度优先搜索(BFS):Java实现

摘要：图的搜索，深度优先搜索，广度优先搜索，DFS,BFS，Java实现

一、背景知识：

（1）图的表示方法：邻接矩阵（二维数组）、邻接表（链表数组【链表的链表】）。

（2）图的搜索方法：深度优先搜索（DFS）和广度优先搜索（BFS）。

二、图的搜索：

1、深度优先搜索（DFS）：

深度优先搜顾明思议是一条道走到黑，走到走不下去了再回过头来从新选择继续走，其实是回溯法的思想。我们这里用的技巧是栈，栈后进先出的性质刚好适用于深度优先搜索。步骤如下：

1、初始搜索点入栈，并标记它已搜索成功
2、如果栈不为空，则访问栈顶元素相邻的一个未标记为已搜索的顶点，若存在则标记它，并入栈
3、如果栈不为空，却不能执行2，则从栈中弹出一个顶点
4、如果不能执行2和3，则搜索结束

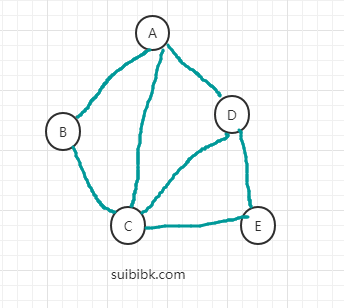
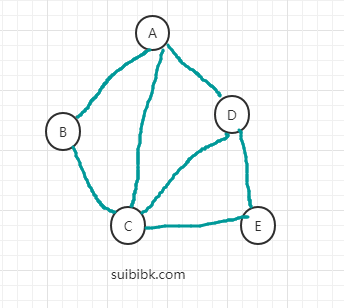
举个例子，比如上图的一个深度优先搜索，假设初始搜索点为A，栈为S。

第一步：A入栈，标记A已搜索，此时栈S={A}。搜索A成功。
第二步：栈不为空，访问A的一个未标记为已搜索相邻的的顶点，这里是B，此时S={A,B}。搜索成功B。
第三步：访问B的一个未标记为已搜索相邻的的顶点，这里是C，此时S={A,B,C}。搜索成功C。
第四步：访问C的一个未标记为已搜索相邻的的顶点，这里是E，此时S={A,B,C,E}。搜索成功E。
第五步：访问E的一个未标记为已搜索相邻的的顶点，这里是D，此时S={A,B,C,E,D}。搜索成功D。
第六步：访问D的一个未标记为已搜索相邻的的顶点，未找到，弹出D，此时S={A,B,C,E}。
第七步：访问E的一个未标记为已搜索相邻的的顶点，未找到，弹出E，此时S={A,B,C}。
第八步：访问C的一个未标记为已搜索相邻的的顶点，未找到，弹出C，此时S={A,B}。
第九步：访问B的一个未标记为已搜索相邻的的顶点，未找到，弹出B，此时S={A}。
第十步：访问A的一个未标记为已搜索相邻的的顶点，未找到，弹出A，此时S={}。
第十一步：栈为空，搜索结束。

搜索结果为：A,B,C,E,D

2、广度优先搜索

广度优先搜索，顾名思义就是先把旁边的都搜索完再向前进，其实这个是分支限界发的思想，我们这里用的技巧是队列，队列的先进先出的性质刚好适用于广度优先搜索。步骤如下：

1、初始搜索点入队列，并标记它已搜索成功
2、若队列不为空，则找到队头未标记为已搜索相邻的顶点，若存在，则标记为已搜索，继续执行这一步。
3、若2不能执行，则队头出对列，继续执行2.
4、若队列为空则搜索结束。

举个例子，比如上图的一个广度优先搜索，假设初始搜索点为A，队列为Q

第一步：A入队列，标记A已搜索，此时对队列为Q={A}。
第二步：则找到队头A未标记为已搜索相邻的顶点B,标记B为已搜索，此时队列为Q={A,B}。
第三步：继续找到队头A未标记为已搜索相邻的顶点C,标记C为已搜索，此时队列为Q={A,B,C}。
第四步：继续找到队头A未标记为已搜索相邻的顶点D,标记C为已搜索，此时队列为Q={A,B,C,D}。
第五步：继续找到队头A未标记为已搜索相邻的顶点，此时找不到，则对头出队列Q={B,C,D}。输出A。
第六步：继续找到队头B未标记为已搜索相邻的顶点,此时找不到，则对头出队列Q={C,D}。输出B。
第七步：继续找到队头C未标记为已搜索相邻的顶点D,标记C为已搜索，此时队列为Q={C,D,E}。
第八步：继续找到队头C未标记为已搜索相邻的顶点,此时找不到，则对头出队列Q={D,E}。输出C。
第九步：继续找到队头D未标记为已搜索相邻的顶点,此时找不到，则对头出队列Q={E}。输出D。
第十步：继续找到队头E未标记为已搜索相邻的顶点,此时找不到，则对头出队列Q={}。输出E。
第十一步：队列为空，搜索结束。

搜索结果为：A,B,C,D,E

三、Java实现

经过上面的分析，相信很容易就能够写出代码来了，我下面是自己封装了一个栈和一个队列，并且队列是静态的，用数组实现。

/**
 * 深度优先搜索，广度优先搜索
 * @author suibibk@qq.com
 */
public class DFS_BFS_SEARCH {
    public static void main(String[] args) {
        Graph graph = new Graph(5);
        graph.addVertex("A");
        graph.addVertex("B");
        graph.addVertex("C");
        graph.addVertex("D");
        graph.addVertex("E");
        graph.addEdge("A", "B");
        graph.addEdge("A", "C");
        graph.addEdge("A", "D");
        graph.addEdge("B", "C");
        graph.addEdge("C", "E");
        graph.addEdge("E", "D");
        graph.addEdge("C", "D");
        System.out.println("输出该图G：");
        graph.print();
        System.out.println("深度优先搜索从A开始:");
        graph.dfs("A");
        System.out.println();
        System.out.println("深度优先搜索从E开始:");
        graph.dfs("E");
        System.out.println();
        System.out.println("广度优先搜索从A开始:");
        graph.bfs("A");
        System.out.println();
        System.out.println("广度优先搜索从E开始:");
        graph.bfs("E");
    }
}
//定义图：无向图
class Graph{
    //顶点数目
    int size;
    //顶点
    List<String> vertexs;
    //边
    int[][] edges;
    //被访问的接地那，0是未被访问，1是已被访问
    int[] visited;
    //初始化
    public Graph(int size) {
        this.size=size;
        this.vertexs=new ArrayList<String>(size);
        this.edges=new int[size][size];
        this.visited=new int[size];
    }
    //添加顶点
    public void addVertex(String vertex) {
        vertexs.add(vertex);
    }
    //添加边
    public void addEdge(String vertex1,String vertex2) {
        int index1 = this.getPosition(vertex1);
        if(index1==-1) {
            System.out.println("顶点"+vertex1+"不存在");
            return;
        }
        int index2 = this.getPosition(vertex2);
        if(index2==-1) {
            System.out.println("顶点"+vertex1+"不存在");
            return;
        }
        //因为是无向图，所以这里直接把两条边都加上
        edges[index1][index2]=1;
        edges[index2][index1]=1;
    }
    //获取顶点对应的坐标
    public int getPosition(String vertex) {
        for (int i = 0; i <size; i++) {
            if(vertexs.get(i).equals(vertex)) {
                return i;
            }
        }
        //没有则返回-1 
        return -1;
    }
    /***************上面已经做好了图，现在做遍历********************/
    /**
     * 输出节点
     * @param index
     */
    public void display(int index ) {
        System.out.println("visit:"+vertexs.get(index));
    }
    /**
     * 打印图
     * @param index
     */
    public void print() {
        System.out.print("G ");
        for (String vertex: vertexs) {
            System.out.print(vertex+" ");
        }
        System.out.println();
        for (int i = 0; i <size; i++) {
            String vertex = vertexs.get(i);
            System.out.print(vertex+" ");
            for (int j = 0; j < size; j++) {
                System.out.print(edges[i][j]+" ");
            }
            System.out.println();
        }
        System.out.println();
    }
    /**
     * 获取节点index相邻的且没有被访问过的节点下标，没有返回-1
     * @param index
     * @return
     */
    public int getAdjacentVertexIndex(int index) {
        for (int j = 0; j < size; j++) {
            if(edges[index][j]==1&&visited[j]!=1) {
                return j;
            }
        }
        return -1;
    }
    /**
     * 深度优先搜索
     * @param start 开始的节点
     */
    public void dfs(String start) {
        int index = this.getPosition(start);
        //1、初始化一个栈
        MyStack stack = new MyStack(size);
        //2、顶点入栈
        stack.push(index);
        //3、标记栈顶为已经访问
        this.display(index);
        visited[index]=1;
        while(!stack.isEmpty()) {
            int v= this.getAdjacentVertexIndex(stack.peek());
            if(v==-1) {
                //如果这个点已经没有邻接顶点了，就弹出
                stack.pop();
            }else {
                //访问到了一个新的节点，直接职标记为已访问
                this.display(v);
                this.visited[v]=1;
                stack.push(v);
            }
        }
        //广度搜索结束后，需要把节点全部变为未搜索，以用于下次搜索
        for (int i = 0; i < size; i++) {
            visited[i]=0;
        }
    }
    /**
     * 广度优先搜索
     * @param start 开始的节点
     */
    public void bfs(String start) {
        int index = this.getPosition(start);
        //1、初始化一个队列
        MyQueue queue = new MyQueue(size);
        //2、顶点入队列
        queue.enqueue(index);
        visited[index]=1;
        while(!queue.isEmpty()) {
            while(true) {
                int v= this.getAdjacentVertexIndex(queue.peek());
                if(v==-1) {
                    //这里表示这个顶点已经没有邻接的了
                    break;
                }else {
                    //访问到了一个新的节点，直接标记为已经访问
                    this.visited[v]=1;
                    queue.enqueue(v);
                }
            }
            //出对列
            int front = queue.dequeue();
            this.display(front);
        }
        //深度搜索结束后，需要把节点全部变为未搜索，以用于下次搜索
        for (int i = 0; i < size; i++) {
            visited[i]=0;
        }
    }
}
/**
 * 深度优先搜索要用到栈，这里自己自定义一个栈，主要操作是
 * 出栈：pop
 * 入栈：push
 * 查看：peek
 * 判空：isEmpty
 */
class MyStack{
    int size;
    int[] stack;
    int top;//栈顶的位置，出栈只能从栈顶出
    //初始化
    public MyStack(int size) {
        this.stack=new int[size];
        this.size=size;
        this.top=-1;
    }
    //入栈
    public void push(int j) {
        if(top+1==size) {
            System.out.println("栈已经满了");
            return;
        }
        stack[++top]=j;
    }
    //出栈
    public int pop() {
        if(top==-1) {
            return -1;
        }
        return stack[top--];
    }
    //查看
    public int peek() {
        return stack[top];
    }
    //判断栈空
    public boolean isEmpty() {
        return (top==-1);
    }
}
/**
 * 定义队列，广度优先搜索要用到队列，队列基本操作
 * 这个是静态队列，一次性的，动态的可以用链表
 * 入队：enqueue
 * 出队：dequeue
 * 查看：peek
 * 判空：isEmpty
 */
class MyQueue{
    int size;
    int[] queue;
    int front;//队头
    int rear;//队尾
    public MyQueue(int size) {
        this.queue=new int[size];
        this.size=size;
        this.front=0;
        this.rear=-1;
    }
    //入队：队尾进入
    public void enqueue(int j) {
        if(rear+1==size) {
            System.out.println("队列已满");
            return;
        }
        queue[++rear]=j;
    }
    //出队:出队从对头出
    public int dequeue() {
        if (!isEmpty()) {
            return queue[front++];
        } else {
            return -1;
        }
    }
    //查看
    public int peek() {
        if (!isEmpty()) {
            return queue[front];
        } else {
            return -1;
        }
    }
    //判空
    public boolean isEmpty() {
        return (rear+1==front);
    }
}

运行结果如下：

输出该图G：
G A B C D E 
A 0 1 1 1 0 
B 1 0 1 0 0 
C 1 1 0 1 1 
D 1 0 1 0 1 
E 0 0 1 1 0 
深度优先搜索从A开始:
visit:A
visit:B
visit:C
visit:D
visit:E
深度优先搜索从E开始:
visit:E
visit:C
visit:A
visit:B
visit:D
广度优先搜索从A开始:
visit:A
visit:B
visit:C
visit:D
visit:E
广度优先搜索从E开始:
visit:E
visit:C
visit:D
visit:A
visit:B

有不足之处，希望大家指正，转载请注明出处。