个人随笔
目录
算法设计技巧之回溯法（Java实现N皇后问题）
2020-04-18 23:01:57

一、基本概念

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。

回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。

二、基本思想

在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根结点出发深度探索解空间树。当探索到某一结点时，要先判断该结点是否包含问题的解，如果包含，就从该结点出发继续探索下去，如果该结点不包含问题的解，则逐层向其祖先结点回溯。

若用回溯法求问题的所有解时，要回溯到根，且根结点的所有可行的子树都要已被搜索遍才结束。而若使用回溯法求任一个解时，只要搜索到问题的一个解就可以结束。

三、解题步骤

（1）针对给定问题，定义问题的解空间树：首先应明确定义问题的解空间，问题的解空间应至少包含问题的一个（最优）解；
（2）确定结点的扩展搜索规则；
（3）以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。

四、算法框架

（1）问题框架

设问题的解是一个n维向量(a1,a2,………,an),约束条件是ai(i=1,2,3,…..,n)之间满足某种条件，记为f(ai)。

（2）非递归回溯框架

  1.  int a[n],i;
  2.  初始化数组a[];
  3.  i = 1;
  4.  while(i>0(有路可走)&&(未达到目标)){  //还未回溯到头
  5.     if(i > n){//搜索到叶结点
  6.         搜索到一个解，输出；
  7.     }else { //处理第i个元素
  8.         a[i]第一个可能的值；
  9.         while(a[i]在不满足约束条件且在搜索空间内) {
  10.             a[i]下一个可能的值；
  11.         }
  12.         if(a[i]在搜索空间内){
  13.             标识占用的资源；
  14.             i = i+1; //扩展下一个结点
  15.          }else {
  16.             清理所占的状态空间 //回溯
  17.             i = i–1; 
  18.         }
  19.     }
  20. }

（3）递归的算法框架

回溯法是对解空间的深度优先搜索，在一般情况下使用递归函数来实现回溯法比较简单，其中i为搜索的深度，框架如下：

  1. int a[n];
  2. try(int i){
  3.    if(i>n){}
  4.            输出结果;
  5.     }else {
  6.         for(j =下界; j <= 上界; j=j+1)   { //枚举i所有可能的路径
  7.              if(fun(j)){                //满足限界函数和约束条件
  8.                 a[i] = j;
  9.                  ...                         //其他操作
  10.                 try(i+1);
  11.                   回溯前的清理工作（如a[i]置空值等）;
  12.             }
  13.           }
  14.     }
  15.   }

四、N皇后问题

八皇后问题：在8*8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

用回溯法求解问题，重点是设计问题的解空间树，其解题过程则是深度遍历解空间树的过程。

解空间树：是依据待求解问题的特性，用树结构表示问题的解结构、用叶子表示问题所有可能的解的一棵树。

解空间树的形成过程：我们可以把求解问题的过程当作一系列的决定来考虑，回溯法对每一个决定都系统地分析所有可能的结果。而每一次决定即为解空间树中的一个分支结点，各种可能的结果便形成了各棵不同的子树，问题最终所有可能的解将展现在所有的叶子上。这便是解空间树的形成过程。

对解空间树的遍历可搜索到问题所有可能的解，因此，可获得满足要求的全部解，也可通过对所有解的比较选择获得最优解。

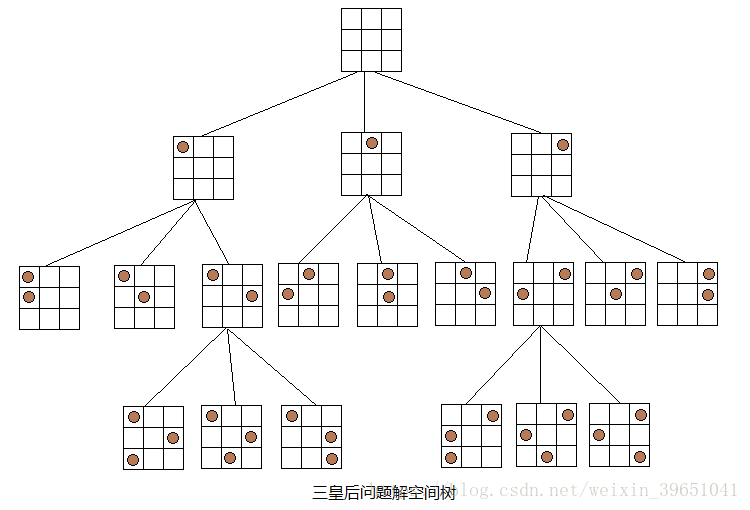
由于空间问题，下面给出一个三皇后问题的解空间树（3皇后问题无解），树中第i层的结点决定第i行皇后的摆放位置，均有三种不同的选择，便形成了三个孩子结点，但其中不包括不符合要求的布局。N皇后问题解空间树与三皇后问题解空间树类似。

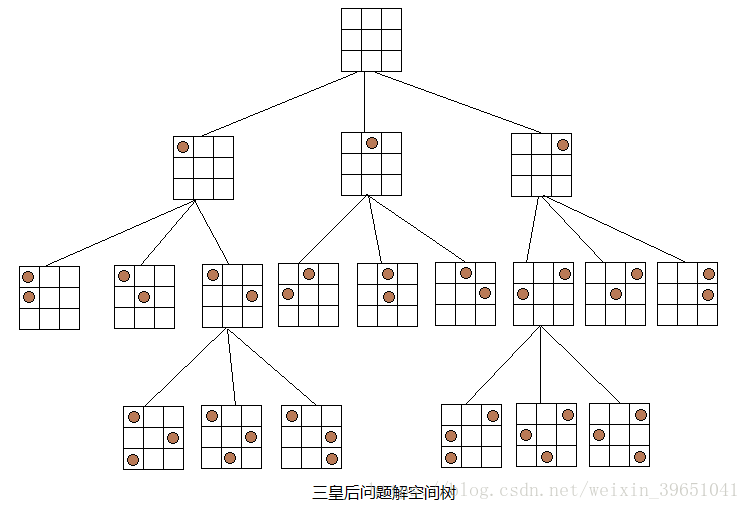
求解N皇后问题的回溯法

N皇后问题要求求解在N*N的棋盘上放置N个皇后，并使各皇后彼此不受攻击的所有可能的棋盘布局。皇后彼此不受攻击的约束条件是：任何两个皇后均不能在棋盘上同一行、同一列或者同一对角线上出现。

由于N皇后问题不允许两个皇后在同一行，所以，可用一维数组X表示N皇后问题的解，X[i]表示第i行的皇后所在的列号。例如一个满足要求的四皇后棋盘布局如下图所示，其结果X数组的值为：[2， 4， 1， 3]。

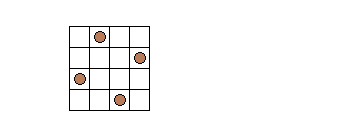
由上述X数组求解N皇后问题，保障了任意两个皇后不在同一行上，而判定皇后彼此不受攻击的其他条件，可以描述如下：

（1）X[i] = X[s]，则第i行与第s行皇后在同一列上。

（2）如果第i行的皇后在第j列，第s行皇后在第t列，即X[i] = j和X[s] = t，则只要i-j = s-t或者i+j = s+t，说明两个皇后在同一对角线上。

对两个等式进行变换后，得到结论：只要|i-s| = |j-t|（即i-s = X[i]-X[s]），则皇后在同一对角线上。

解N皇后问题需要遍历解空间树，遍历中要随时判定当前结点棋盘布局是否符合要求，符合要求则继续向下遍历，直至判断得到一个满足约束条件的叶子结点，从而获得一个满足要求的棋盘布局；不符合要求的结点将被舍弃（称之为剪枝），并回溯到上一层的结点继续遍历。当整棵树遍历结束时，已获得所有满足要求的棋盘布局。

综上所述，用回溯法递归遍历解空间树，求解N皇后问题的算法如下（Java）。

  1. public class NQueens {
  2.     public static List<List<String>> solveNQueens(int n){
  3.         //判断边界条件
  4.         if(n<=0)return null;
  5.         //新建一个特全局变量保存结果
  6.         List<List<String>> res = new ArrayList<>();
  7.         //保每一个皇后的位置的结果变量
  8.         int[] queen = new int[n];
  9.         //进行递归
  10.         backTrack(res,queen,0);
  11.         return res;
  12.     }
  13.     public static void backTrack(List<List<String>> res,int[] queen ,int pos) {
  14.         //这里就表示全部都找完了，第一个已经找到
  15.         if(pos==queen.length){
  16.             List<String> list = new ArrayList<>();
  17.             for(int i=0;i<queen.length;i++){
  18.                 //sb表示每一行的符合条件的结果
  19.                 StringBuilder sb = drawPoint(queen.length);
  20.                 sb.setCharAt(queen[i],'Q');
  21.                 list.add(sb.toString());
  22.             }
  23.             res.add(list);
  24.             return ;
  25.         }
  27.         for (int i = 0; i < queen.length; i++) {
  28.             //循环调用从第一行开始寻找符合条件的皇后的位置
  29.             queen[pos]=i;
  30.             //不满足条件，这一行的皇后向右移
  31.             if(isValid(queen, pos)) {
  32.                 //1、第pos行的皇后已经确定了，现在递归的去找下一行的皇后
  33.                 //2、若是找的到下一行则会继续递归的向下找，直到pos==queen.length则表明这个是满足条件的
  34.                 //递归结束（成功或者失败）后则会返回【回溯】到这个for循环，这一行的皇后向右移
  35.                 backTrack(res, queen, pos+1);
  36.             }
  38.         }
  39.     }
  40.     /**Math.abs(queen[pos]-queen[i])==Math.abs(i-pos)表示对角线
  41.       *  判定条件
  42.      * @param queen
  43.      * @param pos 当前行
  44.      * @return
  45.      */
  46.     public static boolean isValid(int[]queen,int pos){
  47.         for(int i = 0;i<pos;i++){
  48.             if(queen[pos]==queen[i]) return false;
  49.             if(Math.abs(queen[pos]-queen[i])==Math.abs(i-pos)) return false;
  50.         }
  51.         return true;
  52.     }
  53.     public static StringBuilder drawPoint(int n){
  54.         StringBuilder sb = new StringBuilder();
  55.         for(int i = 0 ;i<n ; i++) sb.append("□");
  56.         return sb;
  57.     }
  58.     public static void main(String[] args) {
  59.         List<List<String>> result = solveNQueens(8);
  60.         for (List<String> list : result) {
  61.             for (String str : list) {
  62.                 System.out.println(str);
  63.             }
  64.             System.out.println();
  65.         }
  66.         System.out.println(result.size());
  67.     }
  68. }

将n定义为8，运行结果如下：

  1. Q□□□□□□□
  2. □□□□Q□□□
  3. □□□□□□□Q
  4. □□□□□Q□□
  5. □□Q□□□□□
  6. □□□□□□Q□
  7. □Q□□□□□□
  8. □□□Q□□□□
  9. ...
  10. □□□□□□□Q
  11. □□Q□□□□□
  12. Q□□□□□□□
  13. □□□□□Q□□
  14. □Q□□□□□□
  15. □□□□Q□□□
  16. □□□□□□Q□
  17. □□□Q□□□□
  19. □□□□□□□Q
  20. □□□Q□□□□
  21. Q□□□□□□□
  22. □□Q□□□□□
  23. □□□□□Q□□
  24. □Q□□□□□□
  25. □□□□□□Q□
  26. □□□□Q□□□
  28. 92

时间复杂度

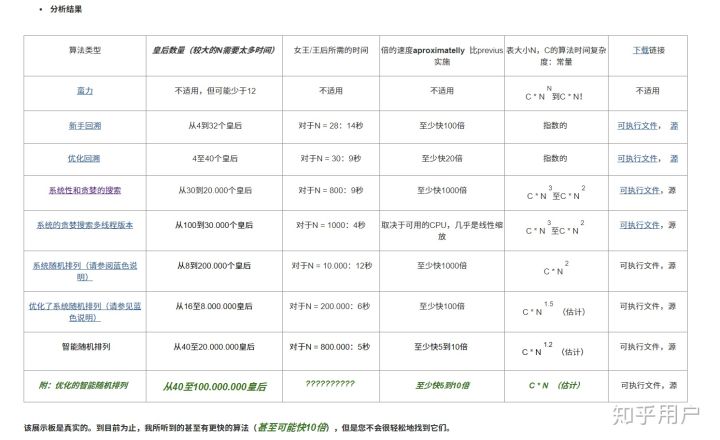
n皇后问题如果不进行任何剪枝，以最朴素的观点来看，其时间复杂度就是O(N^N) 。因为 N 行N 列，皇后的排列方式共有O(N^N)种。下面是一篇总结N皇后问题的复杂度的图，听说还有牛逼的构造算法是O(1).

 485

啊！这个可能是世界上最丑的留言输入框功能~


当然，也是最丑的留言列表

有疑问发邮件到 : suibibk@qq.com 侵权立删
Copyright : 个人随笔   备案号 : 粤ICP备18099399号-2